computacion 8vo B

fracciones

Es la expresión de una cantidad dividida entre otra cantidad ; es decir que representa un cociente no efectuado de números. Por razones históricas también se les llama fracción común, fracción vulgar o fracción decimal. El conjunto matemático que contiene a las fracciones es el conjunto de los números racionales denotado $\mathbb Q$ .

De manera más general, se puede extender el concepto de fracción a un cociente cualquiera de expresiones matemáticas (no necesariamente números).

Numerador y denominador

El Numerador Y El Denominador acciones se componen de: numerador, denominador y línea divisoria entre ambos (barra horizontal u oblicua). En una fracción común $a/b$ el denominador B representa la cantidad de partes iguales en que se ha fraccionado la unidad, y el numerador a es el entero.

NÚMEROS MIXTOS

Un número mixto es la representación de una fracción impropia, en forma de número entero y fracción propia; es una manera práctica de escribir unidades de medidas (peso, tiempo, capacidad), recetas de cocina, etc.

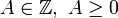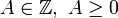Toda fracción impropia $\frac{p}{q}$ puede escribirse como número mixto: $A\$ ^a/_b, en donde $A$ ^a/_b denota $A+\frac{a}{b}$ (donde $A\in \mathbb{Z},~A\geq 0$ , es la parte entera).

Ejemplos:

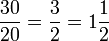$\frac{30}{20}=\frac{3}{2}=1\frac{1}{2}$ «Una cucharadita y media de...»

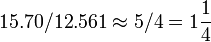$15.70/12.561 \approx 5/4=1\frac{1}{4}$ «En una hora y cuarto...»

A partir de un cierto nivel de álgebra elemental , la notación mixta suele sustituirse por fracciones impropias, que son más operacionales.⁴

Fracción irreducible

Dada una fracción reducible (el numerador y el denominador son primos entre sí), esta siempre se puede reducir ( i .e. simplificar) hasta obtener una fracción equivalente irreducible. La noción de fracción irreducible se generaliza al cuerpo de cocientes de cualquier dominio de factorizado única todo elemento de este cuerpo puede escribirse como una fracción en la cual el numerador y el denominador son con primos

Fracción equivalente

Dos o más fracciones son equivalentes cuando representan la misma cantidad, y se escriben distinto.

Ejemplo:

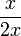las fracciones $\dfrac{1}{2}$ , $\dfrac{2}{4}$ , $\dfrac{3}{6}$ y $\dfrac{x}{2x}$ son equivalentes, ya que representan la cantidad «un medio».

Dos fracciones son equivalentes si pueden obtenerse una a partir de la otra, multiplicando (o dividiendo) por uno.

Ejemplos

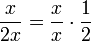$\dfrac{x}{2x}= \dfrac{x}{x} \cdot \dfrac{1}{2}$ en donde $\dfrac{x}{x}=1$ .

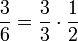$\dfrac{3}{6}= \dfrac{3}{3} \cdot \dfrac{1}{2}$ en donde $\dfrac{3}{3}=1$ .

El conjunto de todas las fracciones equivalentes a una fracción dada, se llama número racional, y suele representarse por la única fracción equivalente irreducible del conjunto.

Bibliografia

WIKIPEDIA (2013) Historia de las matemáticas( 25 de octubre de 2013 ) http://es.wikipedia.org/wiki/Fracci%C3%B3n

computacion 8vo B

viernes, 25 de octubre de 2013

Numerador y denominador

El Numerador Y El Denominador acciones se componen de: numerador, denominador y línea divisoria entre ambos (barra horizontal u oblicua). En una fracción común $a/b$ el denominador B representa la cantidad de partes iguales en que se ha fraccionado la unidad, y el numerador a es el entero.

NÚMEROS MIXTOS

Fracción irreducible

Fracción equivalente

1 comentario:

viernes, 25 de octubre de 2013

Numerador y denominador

El Numerador Y El Denominador acciones se componen de: numerador, denominador y línea divisoria entre ambos (barra horizontal u oblicua). En una fracción común el denominador B representa la cantidad de partes iguales en que se ha fraccionado la unidad, y el numerador a es el entero.

NÚMEROS MIXTOS

Fracción irreducible

Fracción equivalente

1 comentario:

El Numerador Y El Denominador acciones se componen de: numerador, denominador y línea divisoria entre ambos (barra horizontal u oblicua). En una fracción común $a/b$ el denominador B representa la cantidad de partes iguales en que se ha fraccionado la unidad, y el numerador a es el entero.